【工業熱力学】比熱と理想気体(完全ガス)の状態方程式

こんにちは、Xenoです！

今回は『比熱と理想気体(完全ガス)の状態方程式』について解説します。

熱力学で扱う作動流体の一つに理想気体というものがあります。

この理想気体は理論を考えるうえで便利な性質をたくさん持っており、今後はこの理想気体を中心に話を進めていくことになります。

今回の記事を読めば等容比熱や等圧比熱、そして理想気体の状態方程式について理解することができます。

それでは始めましょう！

前回の記事はこちらからどうぞ！

理想気体(完全ガス)とは何か？

熱機関を用いて熱を仕事に変換するとき、作動流体として色々な気体が用いられます。

気体は主に2種類に分けることができ、それが『理想気体(完全ガス)』と『実在気体(蒸気)』です。

理想気体(完全ガス)

理想気体(完全ガス)は、分子間力や分子の体積が無い気体です。

衝撃時には完全弾性反射と仮定されます。

実在気体(蒸気)

実在気体(蒸気)は、分子間力や分子の体積を無視できない気体です。

この気体は分子間で頻繁に衝突が発生しています。

ボイル・シャルルの法則

理想気体においては、以下の法則が成り立つことが分かっています。

ボイルの法則(マリオットの法則)

温度が一定であるとき、圧力は容積に反比例するという法則を、『ボイルの法則(マリオットの法則)』といいます。

この法則は以下の式で表すことができます。

\[pV=(一定)\]

シャルルの法則(ゲイリュサックの法則)

圧力が一定であるとき、容積は温度に比例するという法則を『シャルルの法則(ゲイリュサックの法則)』といいます。

この法則は、以下の式で表すことができます。

\[\frac{V}{T}=(一定)\]

ボイル・シャルルの法則

先ほど紹介したボイルの法則とシャルルの法則を組み合わせた法則を『ボイル・シャルルの法則』と言います。

この法則は、以下の式で表すことができます。

\[\frac{pV}{T}=(一定)\]

理想気体の状態方程式

ボイル・シャルルの法則から、\(m\)を体積\(V\)の気体の質量として扱うと、次式のように表すことができます。

\[\frac{pV}{mT}=(一定)　or　\frac{pv}{T}=(一定)　(1)\]

この一定の値を『気体定数(ガス定数)』と定義します。

単位は\([J/kgK]\)であり、文字記号は\(R\)で表します。

式(1)を改めて気体定数\(R\)で書き直すと次式のように表されます。

\[pV=mRT　or　pv=RT\]

このような方程式を『理想気体(完全ガス)の状態方程式』と言います。

理想気体の内部エネルギー

ジュールは内部エネルギーの性質を調べるために次のような実験を行いました。

実験方法

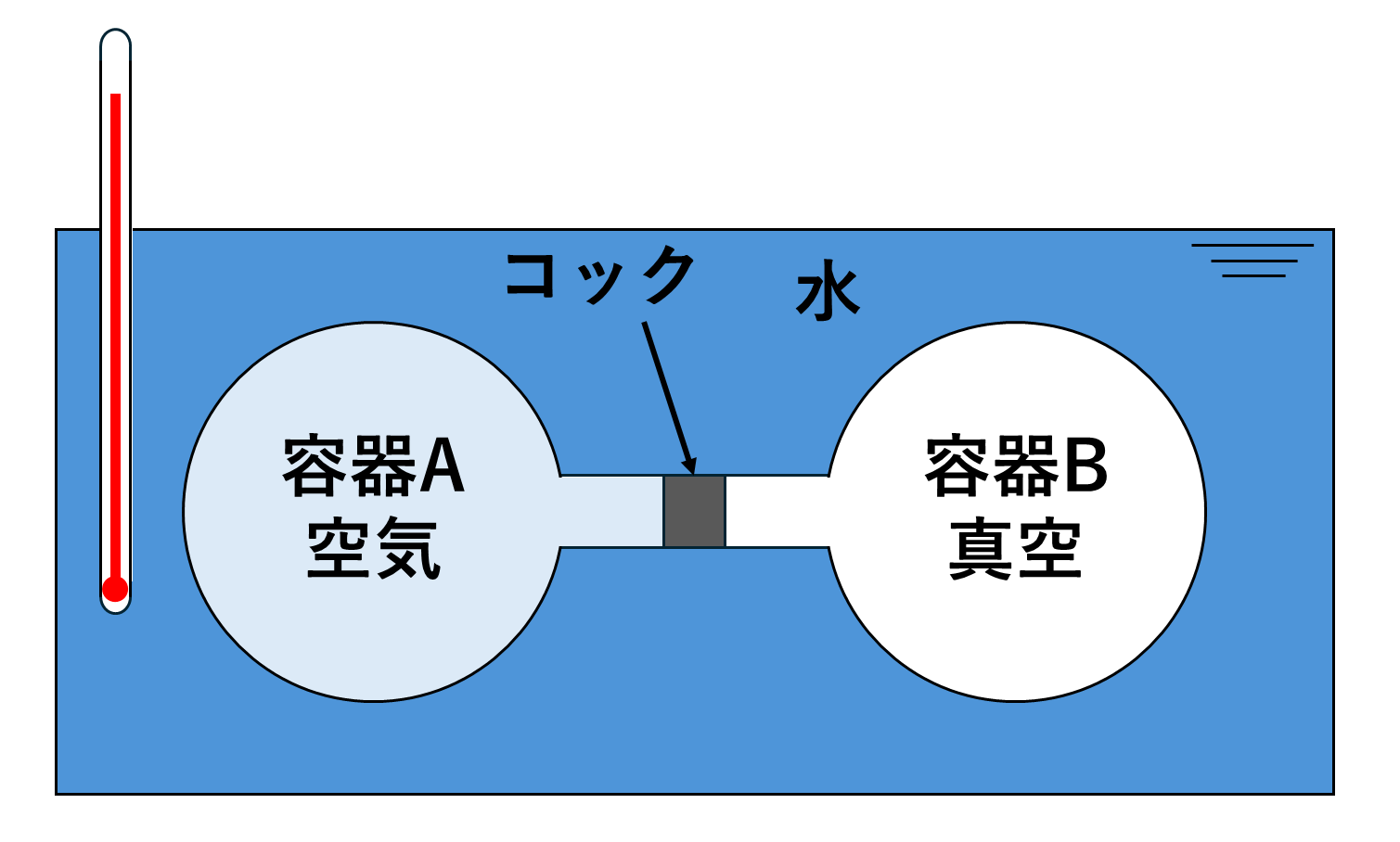
まず、容積の等しい2つの容器をコックを介して繋げて片方に空気を満たし、もう片方は真空にします。

この装置は水の入った容器に入れられており、水温は温度計で図ることができます。

今、コックを開くと片方に満たされていた空気が移動し、容積と圧力が変化します。

ここで温度計で水温を確認するとコックを開く前と水温が変化していないことが確認できます。

このことから熱の移動は無く、自由膨張のため仕事も発生していないことが分かります。

内部エネルギーの性質

以上の結果より、\(dQ=0,dL_a=0\)なので熱力学第一法則から以下のような式が得られます。

\[dQ=dU+dL_a\]

\[dU=0\]

よって、容積\(V\)圧力\(p\)は内部エネルギーに影響しないことが分かります。

つまり、『内部エネルギーは温度のみに依存する関数である』と言えます。

次にエンタルピーについて考えると、理想気体より

\[H=U+pV=U+mRT\]

内部エネルギーは温度の関数であり、\(mR\)は定数なので、『エンタルピーも温度のみに依存する関数』だと言えます。

等容比熱と等圧比熱

比熱\(c[J/kgK]\)は\(1[kg]\)の気体の温度を\(1[℃]\)だけ上昇させるのに必要な熱量なので、比熱を用いて熱量を表すと以下のような式となります。

\[Q=cmdT\]

この式を変形すると次のようになります。

\[c=\frac{dQ}{mdT}=\frac{dq}{dT}[J/kgK]　(2)\]

次に等容変化\(dV=0\)について考えると絶対仕事\(L_a\)は、

\[L_a=\int{pdV}=0\]

となるため、熱力学第一法則より

\[Q=dU+L_a=dU　(3)\]

そして等圧変化\(dp=0\)について考えると工業仕事\(L_t\)は、

\[L_t=-\int{Vdp}=0\]

となるため、熱力学第一法則より

\[Q=dH+L_t=dH　(4)\]

以上より、等容比熱を\(c_v\)、等圧比熱を\(c_p\)として式(3)、(4)を式(2)に代入すれば、以下の関係式を得られます。

\[c_v=\frac{dq}{dT}=\frac{du}{dT}\]

\[du=c_vdT　dU=mc_vdT　(5)\]

\[c_p=\frac{dq}{dT}=\frac{dh}{dT}\]

\[dh=c_pdT　dH=mc_pdT　(6)\]

この2つの関係式は理想気体であればどのような状態変化でも用いることができます。

なぜなら、内部エネルギーエンタルピーは温度にのみ依存する関数であり、\(pV\)線図における等温線上であれば、どこでも内部エネルギーとエンタルピーは等しいからです。

マイヤーの関係式と比熱比

マイヤーの式

ここで、等圧比熱と等容比熱の差を考えてみましょう。

式(5)と(6)の関係式と理想気体の状態方程式を用いると次のような関係式を得ることができます。

以上より、

\[R=c_p-c_v\]

この式を『マイヤーの式』といいます。

比熱比

ここで『比熱比\(\kappa\)』を以下のように定義します。

\[\kappa=\frac{c_p}{c_v}\]

この比熱比の式を変形すると

\[c_p=\kappa{c_v}　(7)\]

ここで、式(7)をマイヤーの式に代入すると以下のような関係式を得ることができます。

\[R=c_p-c_v=c_v(\kappa-1)\]

\[c_v=\frac{R}{\kappa-1}\]

\[c_p=\frac{\kappa{R}}{\kappa-1}\]

以上より、等容比熱と等圧比熱は気体定数と比熱比のみを用いて表すことができることが分かりました。

まとめ

今回は『比熱と理想気体(完全ガス)の状態方程式』について解説しました。

こと理想気体においては、今回解説した状態方程式を活用して問題を解き進めることができます。

等容比熱や等圧比熱の式も重要なのでしっかり把握しておきましょう。

次回は『等圧変化と等容変化』について解説します。

それでは、また次の記事でお会いしましょう！