こんにちは、Xenoです!
今回は『等圧変化と等容変化』について解説します。
前回等圧比熱と等容比熱について紹介しましたが、そもそも等圧変化や等容変化にはどのような特徴があるのでしょうか?
この記事を読めば各変化における絶対仕事や工業仕事、熱量の導き方を理解することができます。
それでは始めましょう!
前回の記事はこちらからどうぞ!

等圧変化
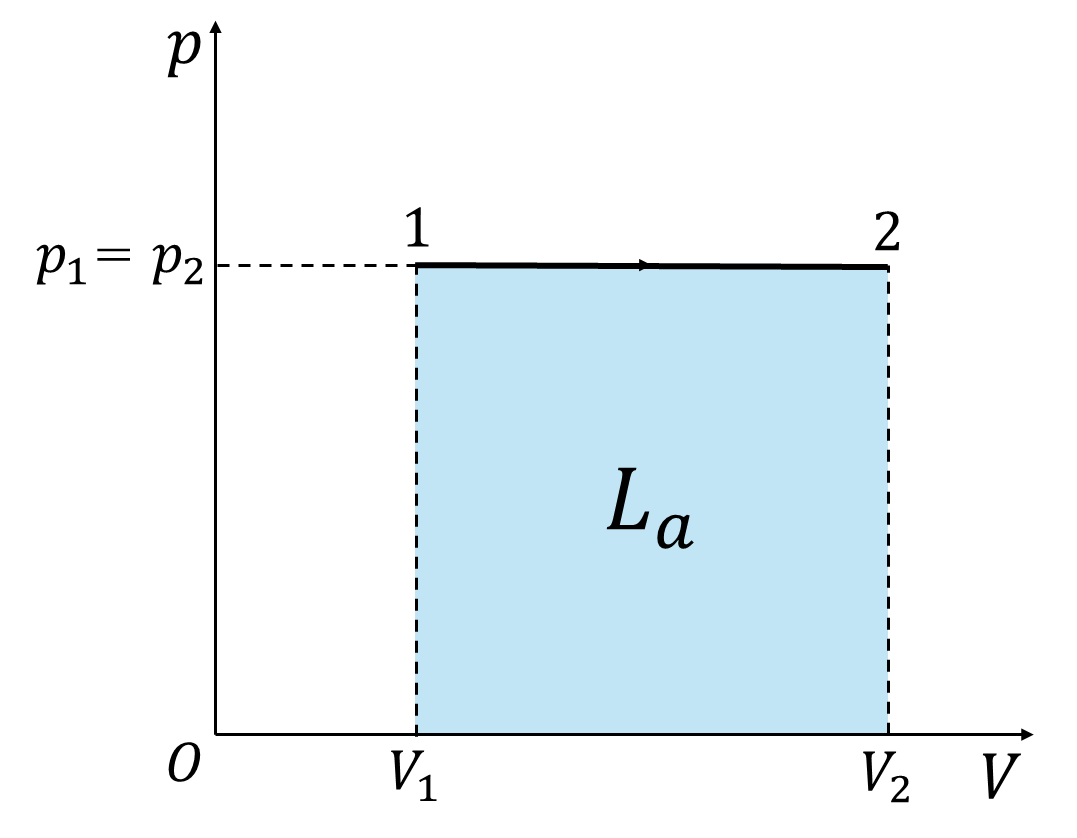
まず、状態変化の過程で圧力が変化しない『等圧変化』を考えます。
理想気体の状態方程式から次式のような関係式が得られることが分かります。
\[pV=mRTより、\]
\[\frac{V_1}{T_1}=\frac{V_2}{T_2}=(一定) (1)\]
絶対仕事
等圧変化は\(p=p_1=p_2=\)(一定)のため、絶対仕事の定義から次のように表すことができます。
\[L_a=\int_1^2{pdV}=p_1\int_1^2{dV}=p_1(V_2-V_1) (2)\]
ここで式(1)を変形すると、
\[\frac{V_1}{T_1}=\frac{V_2}{T_2}\]
\[V_2=\frac{T_2}{T_1}V_1 (3)\]
これを式(2)に代入して、理想気体の状態方程式に当てはめると、
\[L_a=p_1(V_2-V_1)=p_1\left(\frac{T_2}{T_1}V_1-V_1\right)=p_1V_1\left(\frac{T_2}{T_1}-1\right)=mRT_1\left(\frac{T_2}{T_1}-1\right)=mR(T_2-T_1)\]
工業仕事
等圧変化は\(dp=0\)のため、工業仕事の定義から次のように表されます。
\[L_t=-\int_1^2Vdp=0\]
熱量
比熱の定義から等圧比熱\(c_p\)は、
\[c_p=\frac{dq}{dT}=\frac{dh}{dT}\]
なので、エンタルピー変化\(dH\)は、
\[dH=mdh=mc_pdT (4)\]
開いた系の熱力学第一法則の式より工業仕事は0なので、
\[Q_{12}=dH+L_t=dH\]
となり、熱量\(Q_{12}\)はエントロピー変化\(dH\)で表せるので式(4)より、
\[Q_{12}=dH=mc_pdT=mc_p(T_2-T_1)\]
等圧変化の練習問題
問題
\(20\)[℃]の空気\(3[kg]\)を等圧膨張変化させて体積を2倍にするには何℃まで温度を上げれば良いか求めなさい。また、外部になした仕事と加熱量も求めなさい。ただし、空気の気体定数は\(R=287.1[J/kgK]\)、比熱比は\(\kappa=1.4\)とする。
解答と解説
体積は2倍変化したので\(V_2=2V_1\)である。
ここで、この変化は等圧膨張であるのでシャルルの法則より温度\(T_2\)は、
\[T_2=T_1\left(\frac{V_2}{V_1}\right)=293.15×2=586[K]=313[^{\circ}C]\]
また、絶対仕事\(L_a\)は、
\[L_a=mR(T_2-T_1)=3×287.1(313-20)=2.52×10^5[J]=252[kJ]\]
工業仕事\(L_t\)は等圧変化なので
\[L_t=0[J]\]
最後に加熱量\(Q_{12}\)は
\[Q_{12}=mc_p(T_2-T_1)=\frac{m\kappa{R}}{\kappa-1}(T_2-T_1)=\frac{3×1.4×287.1}{1.4-1}(313-20)=883[kJ]\]
等容変化
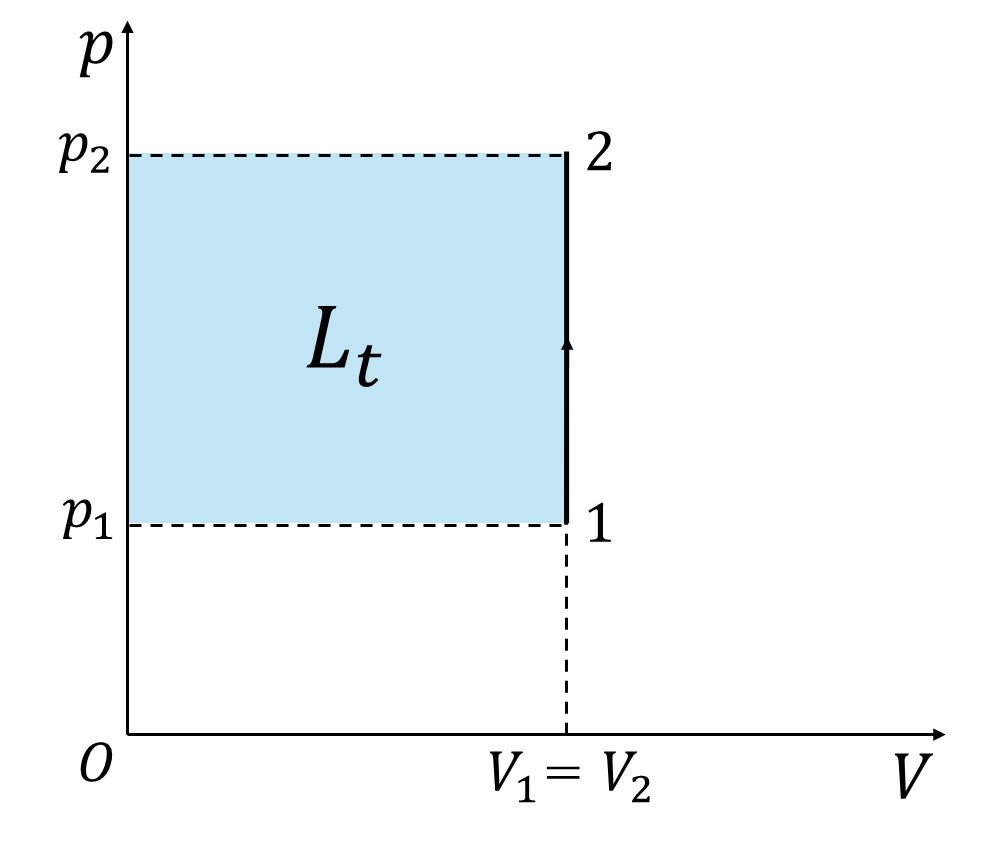
次に、状態変化の過程で容積が変化しない『等容変化』を考えます。
理想気体の状態方程式から次式のような関係式を得られることが分かります。
\[pV=mRTより、\]
\[\frac{p}{T}=\frac{p_1}{T_1}=\frac{p_2}{T_2}=(一定) (5)\]
絶対仕事
等容変化は\(dV=0\)のため、絶対仕事の定義から次のように表されます。
\[L_a=\int_1^2{pdV}=0\]
工業仕事
等容変化は\(V=V_1=V_2=(一定)\)のため、工業仕事の定義から次のように表すことができます。
\[L_t=-\int_1^2{Vdp}=-V\int_1^2{dp}=-V_1(p_2-p_1)=V_1(p_1-p_2) (6)\]
ここで式(5)を変形すると、
\[\frac{p_1}{T_1}=\frac{p_2}{T_2}\]
\[p_2=\frac{T_2}{T_1}p_1 (7)\]
これを式(6)に代入して、理想気体の状態方程式を当てはめると、
\[L_t=V_1(p_1-p_2)=V_1\left(p_1-\frac{T_2}{T_1}p_1\right)=p_1V_1\left(1-\frac{T_2}{T_1}\right)=mRT_1\left(1-\frac{T_2}{T_1}\right)=mR(T_1-T_2)\]
熱量
比熱の定義から等容比熱\(c_v\)は、
\[c_v=\frac{dq}{dT}=\frac{du}{dT}\]
なので、内部エネルギー変化\(dU\)は
\[dU=mc_vdT (8)\]
閉じた系の熱力学第一法則の式より、
\[Q_{12}=dU+L_a=dU\]
となり、熱量\(Q_{12}\)は内部エネルギー変化\(dU\)で表せるので式(8)より、
\[Q_{12}=dU=mc_vdT=mc_v(T_2-T_1)\]
等容変化の練習問題
問題
\(15\)[℃]の空気\(2[kg]\)を等容変化させて圧力を2倍にするには何℃まで温度を上げれば良いか求めなさい。また、外部になした仕事と加熱量も求めなさい。ただし、空気の気体定数は\(R=287.1[J/kgK]\)、比熱比は\(\kappa=1.4\)とする。
解答と解説
圧力は2倍変化したので\(p_2=2p_1\)である。
ここで、この変化は等容変化であるので式(5)より温度\(T_2\)は、
\[T_2=T_1\left(\frac{p_2}{p_1}\right)=288.15×2=576[K]=303[^{\circ}C]\]
また、絶対仕事\(L_a\)は等容変化なので、
\[L_a=0[J]\]
工業仕事\(L_t\)は、
\[L_t=mR(T_1-T_2)=2×287.1(15-303)=-1.65×10^5[J]=-165[kJ]\]
最後に加熱量\(Q_{12}\)は
\[Q_{12}=mc_v(T_2-T_1)=\frac{mR}{\kappa-1}(T_2-T_1)=\frac{2×287.1}{1.4-1}(303-15)=413[kJ]\]
まとめ
今回は『等圧変化と等容変化』について解説しました。
等圧比熱と等容比熱の話で少し出てきたので飲み込みやすかったのではないでしょうか?
逆に前回の比熱の話が理解できなかったという人はひとつ前の記事に戻って確認してみてくださいね。
次回は『等温変化と断熱変化』について解説します。
それでは、また次の記事でお会いしましょう!









コメント