今回は許容応力と安全率について学びましょう。
この材料力学の最初の記事で強度設計について少し触れましたが、今回の内容は、その強度設計においてかなりキーとなるものです。
しっかり学習していきましょう。
前回の記事はこちらからどうぞ!

許容応力
機械などを設計するときには材料力学の知識を使って応力を計算し、その値が条件に耐えられるかを確認します。
ここでいう条件は荷重やその機械が使用される環境(温度や湿度など)、そして実際にその機械が使用される期間を指しています。
設計をする目的は、部品が壊れないのはもちろんのこと、弾性を維持しつつ大きな変形が発生しない範囲で応力が限界を超えないようにすることにあります。
強度設計のおおまかな流れは以下の記事で詳しく解説しています。

しかし、できる限り少ない材料で寸法を小さくしたり、軽量化を図ることでコストを下げることも大切です。
このとき、設計上の応力は、許容できる最大応力に近い方が効率的です。
この、許容できる最大の応力を『許容応力』といいます。
許容応力は、荷重の種類に応じて決められた『基準強さ(基準応力)』を『安全率』で割ることによって求められます。
\[許容応力:\sigma_a=\frac{ \sigma_s }{ f } \begin{cases}{\sigma_s:基準強さ(基準応力)} \\{f:安全率}\end{cases}\]
安全率
安全率は基準強さを決める際に考慮される補正値で、通常1より大きい数値になります。
これは主に以下の様なさまざまな要因によるリスクを補うために設定されます。
- 条件の不確実さ
- 材料に予期しない欠陥が生じる可能性
- 製造時のミス
- 応力計算と実際の状態との違いによる誤差
仮に、実際に使用する材料と全く同じものを使用し、形状や寸法も寸分の狂いもない試験片を作成し、同じ条件下の下で試験を行って基準強さを直接測定できるのであれば、安全率は\(f\fallingdotseq1\)とすることが出来ます。
しかし、現実には実物試験を行うことが非常に困難な場合が大半のため、文献や実験データなどの公表資料を参考にしながら、できるだけ実際の条件に近い基準強さを推定する必要があるのです。
練習問題
問題1
下図のような壁に部材が固定され、力が作用している状態を考える。安全率\(f=1.25\)としたときの許容応力と、伸びを求めなさい。ただし、外径\(d_1=50[mm]\),内径\(d_2=30[mm],l=1500[mm],F=50[kN]\),\(E=206[GPa]\)(軟鋼)とする。
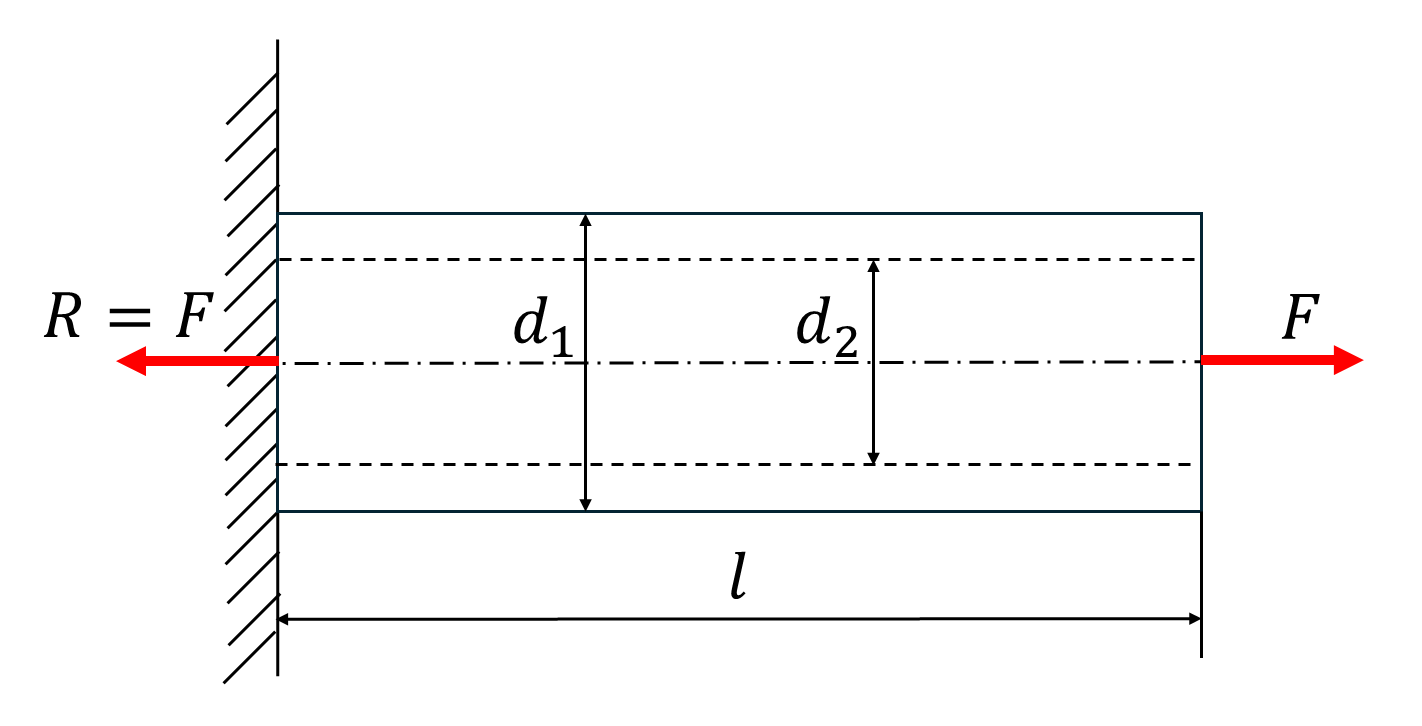
解答と解説1
まず、中空円柱に生じる応力を求めると、
\[\sigma=\frac{F}{A}=\frac{4F}{\pi({d_1}^2-{d_2}^2)}=\frac{4×50×10^3}{\pi\{ (50×10^{-3})^2-(30×10^{-3})^2\}}=39.8[MPa]\]
ここで、安全率から許容応力を求めると、
\[\sigma_a=\frac{\sigma}{f}=\frac{39.8}{1.25}=31.8[MPa]\]
よって、求めたい伸び\(\lambda\)はフックの法則より、
\[\lambda=\frac{\sigma_al}{E}=\frac{31.8×10^6×1500×10^{-3}}{206×10^9}=2.31×10^{-4}[m]=0.231[mm]\]
問題2
下図のように2本の中実丸棒Aが天井に固定されており、片端が中実丸棒Bにそれぞれ固定されている状態を考える。今、丸棒Bの中心に荷重\(F\)が作用するとき、直径\(d_A\)及び\(d_B\)を定めなさい。ただし、引張許容応力\(\sigma_A=80[MPa]\),せん断許容応力\(\tau_B=60[MPa]\),荷重\(F=160[kN]\)とする。
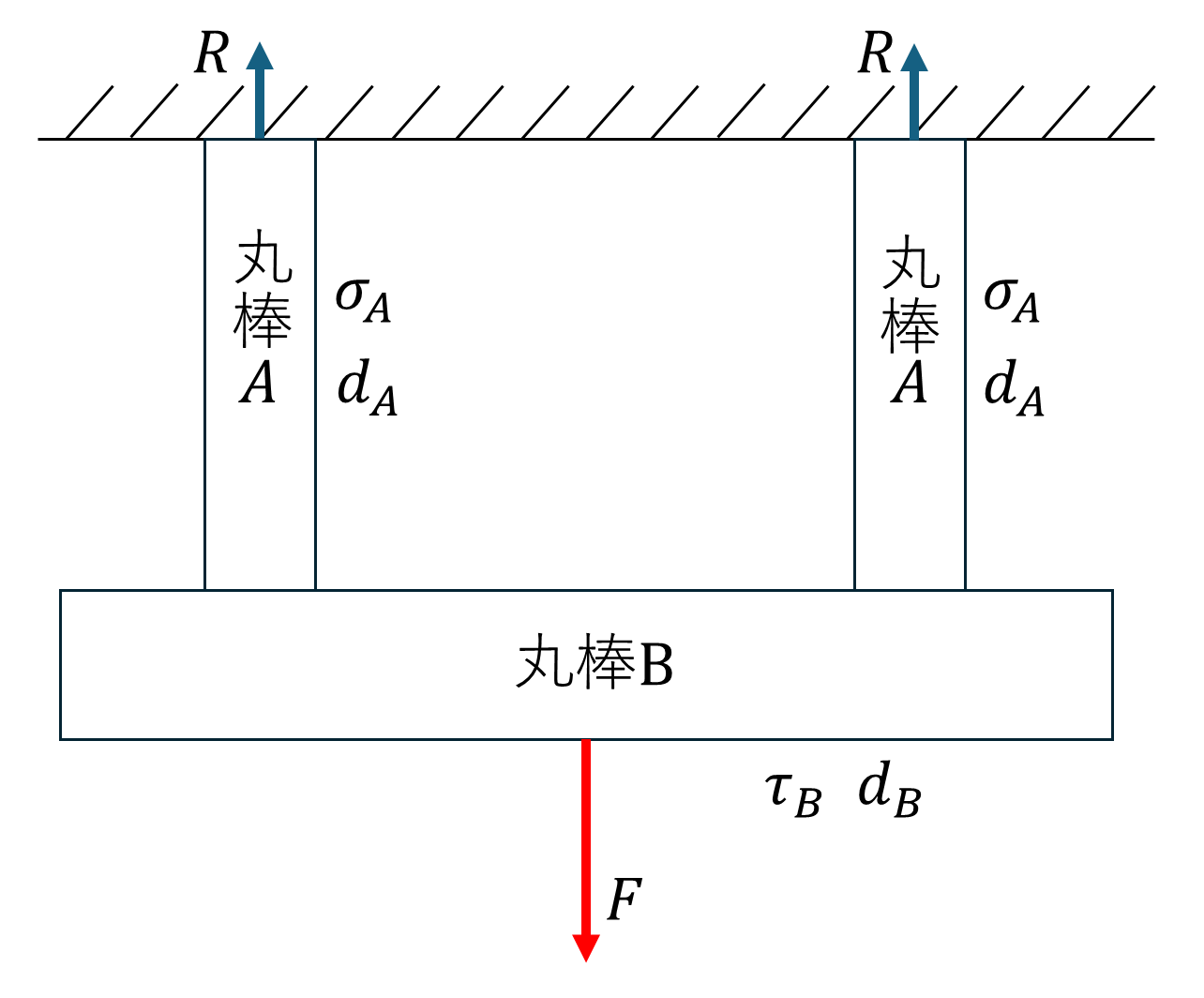
解答と解説2
丸棒Aに作用する力は反力Rに等しいため、力のつりあい式を立てると、
\[{2R=F}\iff{R=\frac{F}{2}}\]よって\[F_A=R=\frac{F}{2}\]
\(F_B\)も同様にして求めると、
\[F_B=\frac{F}{2}\]
よって、それぞれの直径は
\[\sigma_A=\frac{4F_A}{\pi{d_A}^2}=\frac{2F}{\pi{d_A}^2}\]
\[d_A=\sqrt{\frac{2F}{\pi\sigma_A}}=\sqrt{\frac{2×160×10^2}{\pi×100×10^6}}=1.01×10^{-2}[m]=10.1[mm]\]
\[\tau_B=\frac{4F_B}{\pi{d_B}^2}=\frac{2F}{\pi{d_B}^2}\]
\[d_B=\sqrt{\frac{2F}{\pi\tau_B}}=\sqrt{\frac{2×160×10^2}{\pi×60×10^6}}=1.30×10^{-2}[m]=13.2[mm]\]
まとめ
今回は許容応力と安全率ついて解説しました。
今回の内容は説明しても一度では良く分からない人が多いと思ったので、2つの具体的な練習問題を取り上げてみました。
設計において非常に重要な内容なので、しっかり使いこなせるようになりましょう。
次回は「部材の様々な応力と変形」について解説していきます。
ここまで見ていただき、ありがとうございました!









コメント