今回は初期応力と応力集中について学びましょう。
構造物や機械を設計したり加工したりするときには、余計な応力が生じていたり、応力が一か所に集中していないかを確認する必要があります。
この記事を読めばそれらの応力を理解することができるでしょう!
前回の記事はこちらからどうぞ!

初期応力(残留応力)
初期応力(残留応力)とは?
部材に対して外部から荷重が作用していなくても、内部に応力が生じているときがあります。
このような応力を『初期応力(残留応力)』といいます。
初期応力は部材に対して疲労耐久性の低下や変形、歪み、破断、ひび割れなどの様々な問題を引き起こすため、管理や除去が非常に重要です。
発生する要因
初期応力が発生する要因には以下の4つがあります。
機械加工
切削加工や成形加工の際に局所的に発生して、加工部分と非加工部分の間に不均一な応力が生じます。
熱処理・冷却
急激な加熱や冷却によって、材料内部で膨張と収縮の差が生じて、結果として初期応力が発生します。
主に溶接や鋳造の過程での急冷が原因で生じることが多いです。
相変態
金属材料などでは、結晶構造の変化(相変態)によって体積変化が発生して、内部に応力が蓄積されることがあります。
組み立て・圧入
複数の部品を組み合わせる際に、微小な隙間や形状の違いから応力が発生する場合があります。
応力集中
応力集中とは?
部材の形状が急に変化する部分では、その周辺に局所的に大きな応力が発生しやすくなります。
例えば、下図のような板状の部材の途中に丸い穴が空いていると、その穴の周辺に応力が集中しやすくなります。
このような特定の部分に応力が集中する現象を『応力集中』いいます。
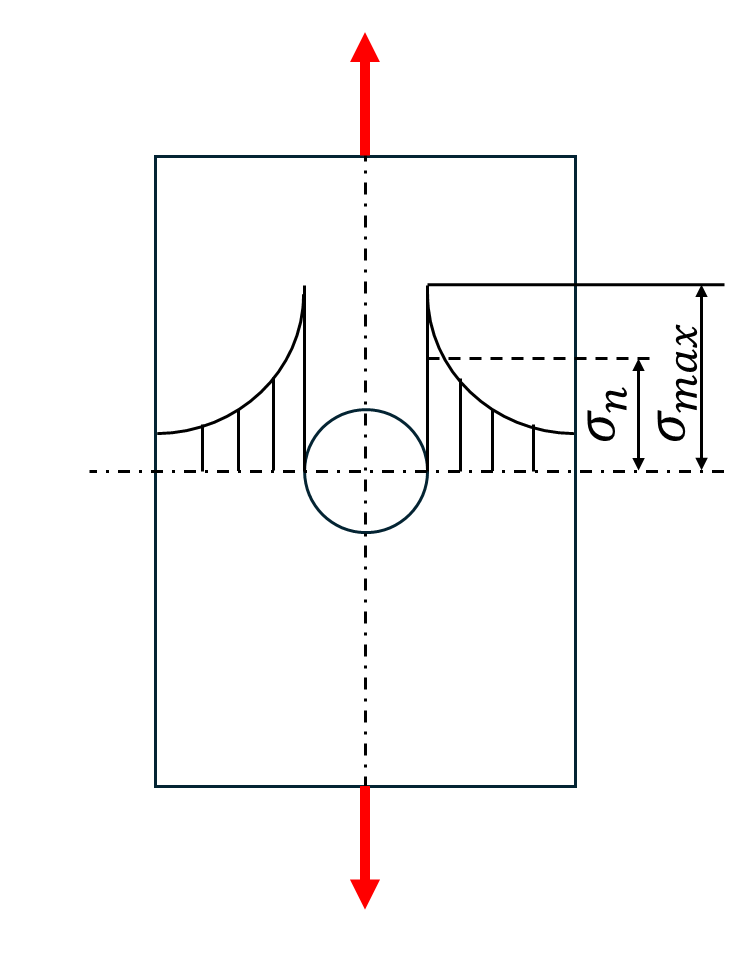
応力集中係数
形状が変化するところは『切欠き』と呼ばれ、切欠きが存在することで応力集中が生じる効果を『切欠き効果』といいます。
切欠きによって生じる最大応力\(\sigma_{max}\)を『集中応力』といい、これに対して切欠きが無い場合の平均的な応力\(\sigma_n\)を『平均応力』といいます。
集中応力と平均応力の比は『応力集中係数』と呼ばれ、次式で表されます。
\[\alpha=\frac{\sigma_{max}}{\sigma_n} \begin{cases}{\sigma_{max}:集中応力[MPa]}\\{\sigma_{n}:平均応力[MPa]}\end{cases}\]
応力集中係数\(\alpha\)は、部材の形状によって決まるため、『形状係数』とも呼ばれています。
応力集中の影響を抑える方法
応力集中の影響を抑えるためには主に以下の3つのことを意識すると良いでしょう。
フィレット(R加工)の追加
鋭い角や急激な断面変化を避け、滑らかな曲線を入れることで、応力集中を緩和できます。
穴や切欠きの形状改善
円や楕円形にすることで、応力集中を均等に分散することが可能です。
段差の緩和
突然の断面変化を避け、緩やかな勾配やテーパーを入れるように意識しましょう。
練習問題
問題
下図のような段付き部材が間隔\(l=1000[mm]\)の壁の間にはめ込まれている状態を考える。ここで、この段付き部材が長さ\(l_0=1001[mm]\)のまま無理やりはめ込まれたとすると、部材の各部分に生じている初期応力\(\sigma_1,\sigma_2\)を求めなさい。ただし、\(d_1=30[mm],d_2=50[mm],l_1=600[mm],\)\(l_2=400[mm],E=206[GPa]\)とする。
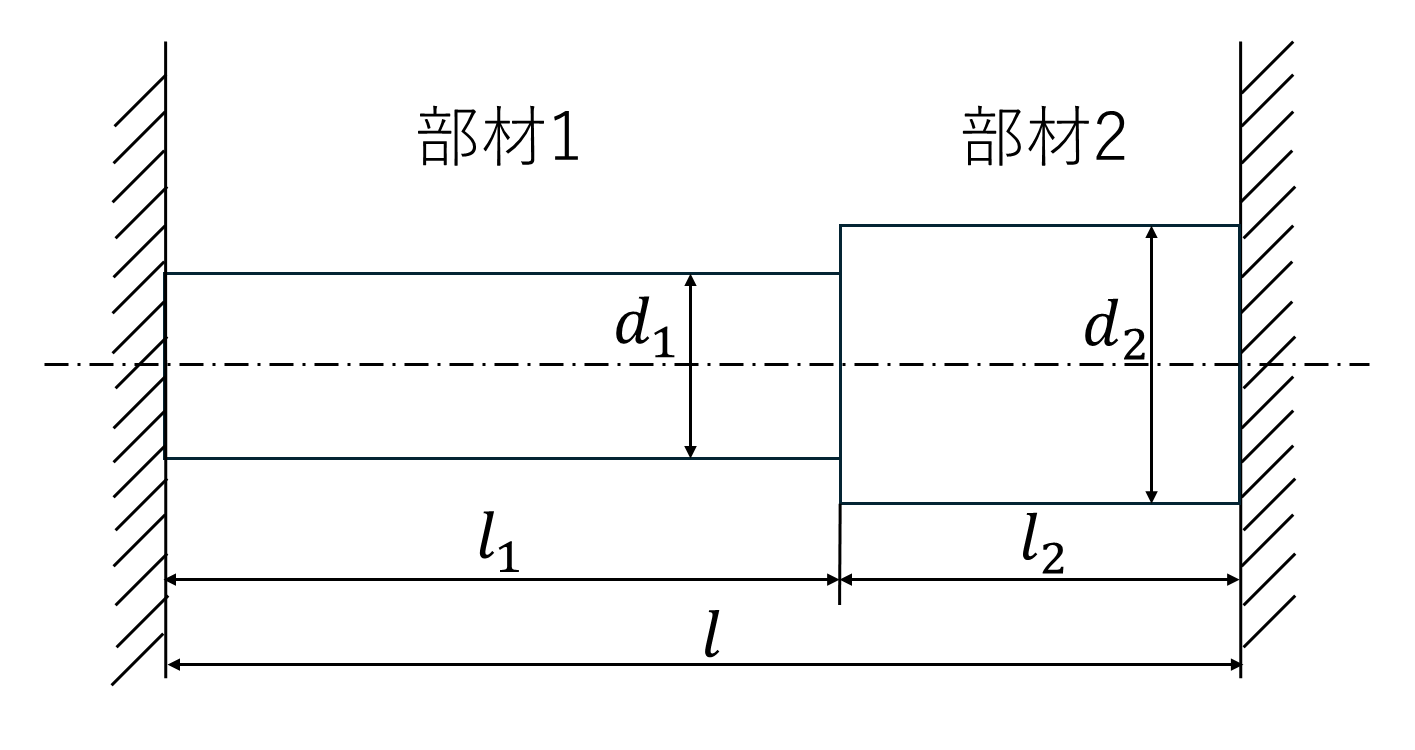
解答と解説
部材1、2に生じる荷重をそれぞれ\(F_1,F_2\)として力のつりあい式を立てると、
\[F_1=F_2\]
\[A_1\sigma_1=A_2\sigma_2\]
\[A_1E\varepsilon_1=A_2E\varepsilon_2\]
ここで、初期応力による各部材の縮みをそれぞれ\(\lambda_1,\lambda_2\)とすると、
\[\frac{\pi{d_1}^2}{4}\frac{\lambda_1}{l_1}=\frac{\pi{d_2}^2}{4}\frac{\lambda_2}{l_2}\]
\[\lambda_1=\frac{{d_2}^2l_1}{{d_1}^2l_2}\lambda_2=\left(\frac{50}{20}\right)^2\frac{600}{400}\lambda_2=4.17\lambda_2\]
はめ込んだことで縮んだ量を\(\lambda\)とすると、
\[\lambda=\lambda_1+\lambda_2=4.17\lambda_2+\lambda_2\]
\[\lambda_2=\frac{\lambda}{5.17}=\frac{1×10^{-3}}{5.17}=0.19×10{-3}[m]=0.19[mm]\]
\[\lambda_1=\lambda-\lambda_2=1-0.19=0.81[mm]\]
よって、求めたい初期応力\(\sigma_1,\sigma_2\)は、
\[\sigma_1=E\varepsilon_1=\frac{E\lambda_1}{l_1}=\frac{206×10^9×0.81}{600}=278[MPa]\]
\[\sigma_2=E\varepsilon_2=\frac{E\lambda_2}{l_2}=\frac{206×10^9×0.19}{400}=97.8[MPa]\]
まとめ
今回は『初期応力(残留応力)と応力集中』について解説しました。
この記事までで材料力学の基礎はある程度学ぶことができます。
まだ理解しきれていない内容があるときは、前の記事に戻って確認してみて下さい。
次回は『真直ばりにおけるせん断力と曲げモーメント』について解説していきます。
ここまで見ていただき、ありがとうございました!








コメント