【材料力学】引張圧縮の不静定問題

2025年3月24日2025年4月16日

今回は引張圧縮の不静定問題について解説します。

今まで部材に荷重が作用したときの反力は力のつりあい式を立てることにより求めることが出来ました。

しかし、それだけで求めることが出来ない問題にはどのように対処すれば良いのでしょうか？

この記事を読むことで不静定問題の解き方を理解することができます。

それでは始めましょう！

前回の記事はこちらからどうぞ！

不静定問題とは何か？

不静定問題とは以下の様な問題のことを言います。

不静定問題 : 未知数を求めるときに力のつりあい式だけでは解を一つに定められない問題

例えば、今までの問題は反力\(R\)を求めようと思ったら力のつりあい式(またはモーメントのつりあい式)を立てればそのまま反力\(R\)を導くことができました。

しかし、これから紹介する不静定問題では二つの未知数(例えば二つの未知の反力\(R_A,R_B\))に対して、力のつりあい式という一つの関係式しか無い為、未知数を求めることができないのです。

では、どうすれば不静定問題を解くことが出来るのでしょうか？

それは、次から説明するいくつかの例題を見ながら考えていきましょう。(ちなみに、今までのように力のつりあいで求められる問題は『静定問題』といいます。)

例題1 部材の両端が固定されたとき

問題

下図のように両端が壁に固定された円柱部材を考えます。ここで点Cの位置で軸方向に荷重Fが作用するとき、壁に生じる反力\(R_A\)、\(R_B\)を求めよ。ただし、\(a=300[mm],b=200[mm],F=50[kN]\)、断面積\(A\)、縦弾性係数\(E\)とする。

解答と解説

まず、今まで通りに力のつりあいを考えると次のようになります。

\[R_A+R_B=F\]

しかし、当然ながら力のつりあい式だけでは2つの反力\(R_A,R_B\)を求めることはできません。

ではどうすれば良いのか？改めて例題の図を見てください。

このように荷重を作用させれば本来、AC部分は伸びて、CB部分は縮むように変形するはずです。

しかし、この部材は両端を固定されているため変形することができません。

よってAC部分、CB部分の伸び\(\lambda_{AC}\)と\(\lambda_{CB}\)の関係は以下の様に表すことができます。

\[\lambda_{AC}=\lambda_{CB}=0\]

上記の式を変形すると、

\[\frac{R_aa}{AE}=\frac{R_Bb}{AE}\]

\[{R_Aa}=R_Bb\]

\[{R_B}=\frac{a}{b}R_A\]

このように、もう一つの反力に関する関係式を導くことができました。

不静定問題は部材の変形を考慮することで解くことができるのです。

上記の関係式を力のつりあい式に代入すると反力を求められます。

\[R_A+\frac{a}{b}R_A=\frac{a+b}{b}R_A=F\]

\[{R_A}=\frac{Fb}{a+b}=\frac{50×200}{300+200}=20[kN]\]

求めた反力\(R_A\)を再び力のつりあい式に代入すれば、

\[R_B=F-R_A=50-20=30[kN]\]

不静定問題は材料の変形に注目することで解くことができる！

例題2 材質の違う部材が固定されたとき

問題

下図のように両端が壁に固定された3本の円柱部材を考える。上下の2本の円柱は材質も直径も等しいものとする。ここで、左右の壁から同じ大きさの荷重\(F\)が作用するとき、それぞれの円柱に生じる反力\(R_1,R_2\)を求めなさい。ただし、\(F=40[kN],d_1=30[mm],d_2=50[mm],E_1=206[GPa],\)\(E_2=96[GPa]\)とする。

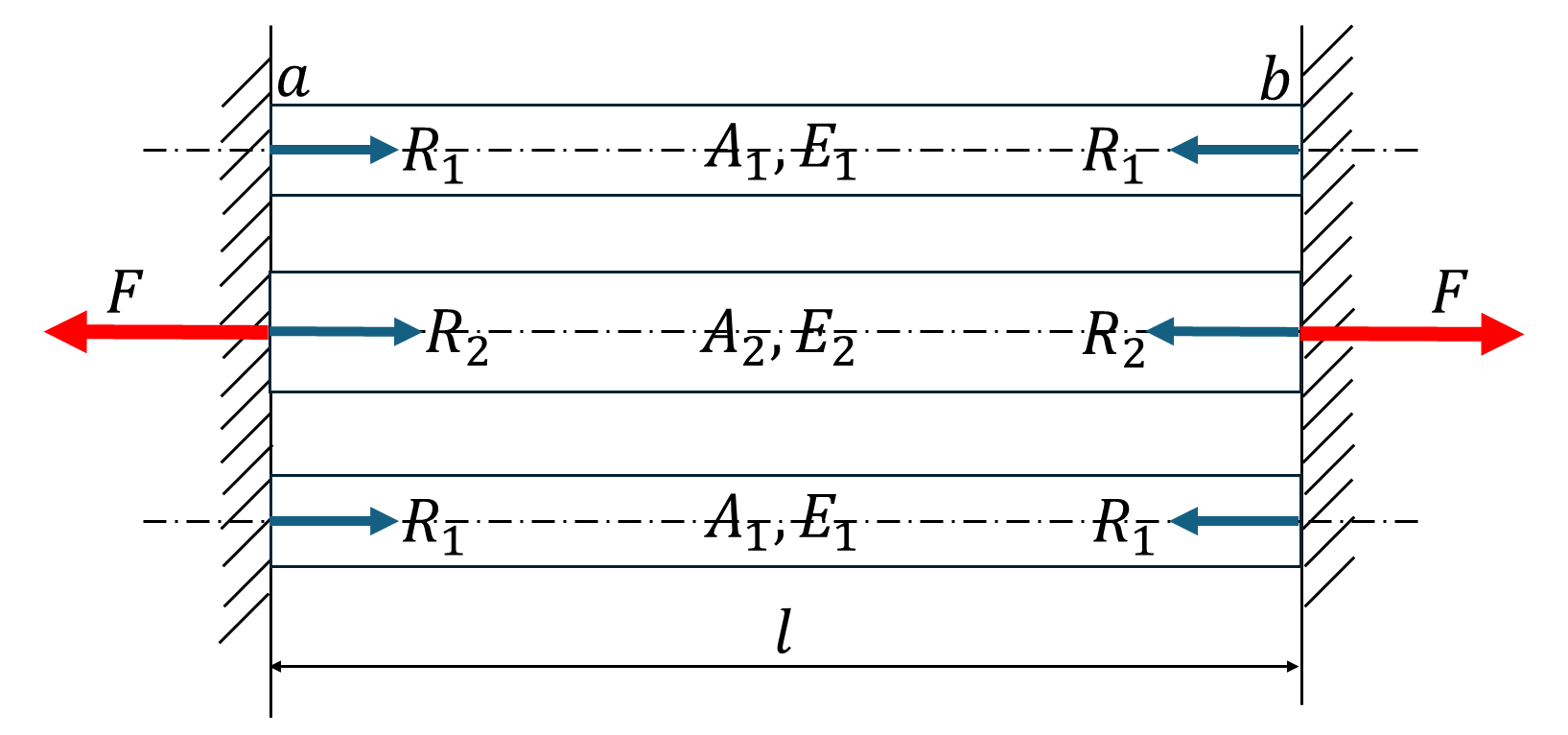
解答と解説

力のつりあい式を考えると、

\[2R_1+R_2=F\]

これも例題1と同様に2つの未知数に対して関係式が一つしかないので、不静定問題であると分かります。

なので、前問と同様に変形を考慮して考えます。

\(\lambda_1=lambda_2=0\)なので、各断面積をそれぞれ\(A_1,A_2\)とすれば、次のような関係式が成り立ちます。

\[\frac{R_1l}{A_1E_1}=\frac{R_2l}{A_2E_2}\]

\[{R_2}=\frac{A_2E_2}{A_1E_1}R_1\]

この式を力のつりあい式に代入すると、

\[2R_1+\frac{A_2E_2}{A_1E_1}R_1=\left(2+\frac{A_2E_2}{A_1E_1}\right)R_1=F\]

スクロールできます

\[{R_1}=\frac{F}{2+\frac{A_2E_2}{A_1E_1}}=\frac{F}{2+\frac{d^2_2E_2}{d^2_1E_1}}=\frac{40×10^3}{2+\frac{(50×10^{-3})^2×96×10^9}{(30×10^{-3})^2×206×10^9}}=12.1[kN]\]

求めた反力\(R_1\)を再び力のつりあい式に代入して、

\[R_2=F-2R_1=40-2×12.1=15.8[kN]\]

練習問題

問題

下図のような円管bの中心に丸棒aが通され、両端を天井と剛体板に固定されている状態を考える。ここで、剛体板の中心に荷重\(F\)が作用するとき、丸棒aと円管bに生じる反力\(R_a,R_b\)と全体の伸び\(lambda\)を求めなさい。ただし、\(d_a=40[mm],d_b=150[mm],l=1000[mm],t=10[mm],F=80[kN],\)\(E_a=206[GPa],E_b=96[GPa]\)とする。

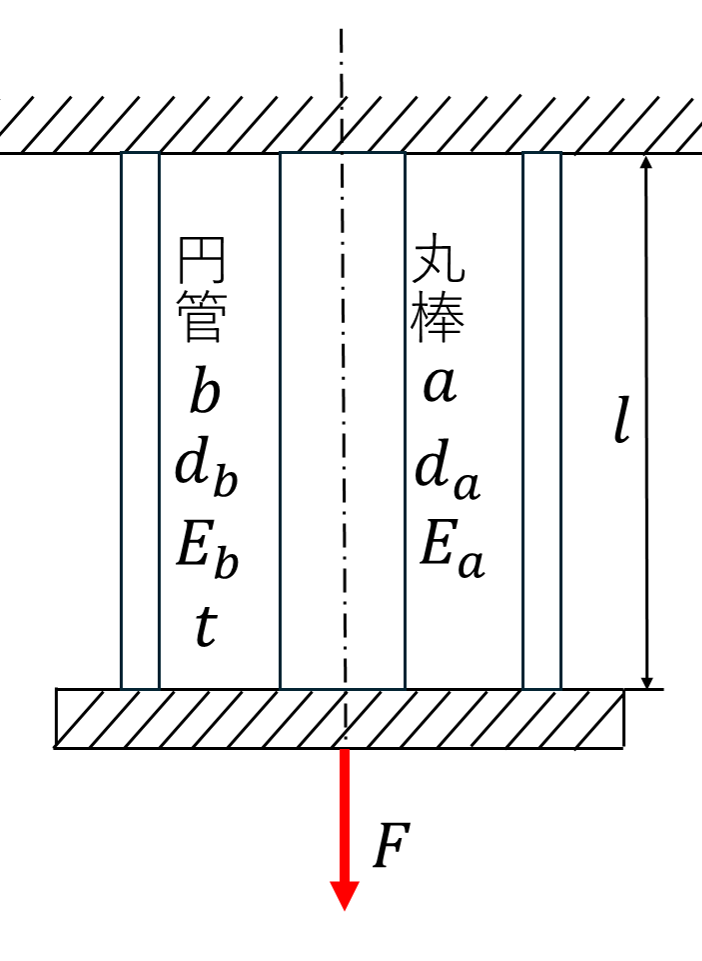
解答と解説

力のつりあい式を立てると、

\[R_a+R_b=F\]

2つの未知数に対して関係式が一つしかないため、不静定問題である。変形を考慮すると\(\lambda=\lambda_a=\lambda_b\)なのでフックの法則より、

\[\frac{R_al}{A_aE_a}=\frac{R_bl}{A_bE_b}\]

\[{\frac{4R_al}{\pi{d^2_a}E_a}}=\frac{4R_bl}{\pi{E_b}\{d^2_b-(d_b-2t)^2\}}\]

\[\frac{R_b}{E_b\{d^2_b-(d_b-2t)^2\}}=\frac{R_a}{d^2_aEa}\]

\[{R_b}=\frac{E_b\{d^2_b-(d_b-2t)^2\}}{d^2_aE_a}R_a\]

この式を力のつりあい式に代入すると、

\[R_a\left(1+\frac{E_b\{d^2_b-(d_b-2t)^2\}}{d^2_aE_a}\right)=F\]

スクロールできます

\[{R_a}=\frac{F}{1+\frac{E_b\{d^2_b-(d_b-2t)^2\}}{d^2_aE_a}}=\frac{80×10^3}{1+\frac{96×10^9\{(150×10^{-3})^2-(150×10^{-3}-2×10^{-3})^2\}}{(40×10^{-3})^2×206×10^9}}=68.2[kN]\]

求めた反力\(R_a\)を力のつりあい式に代入すると、

\[R_b=F-Ra=80-68.2=11.8[kN]\]

よって、全体の伸び\(\lambda\)は、

スクロールできます

\[\lambda=\lambda_a=\lambda_b=\frac{4R_al}{\pi{d}^2_aE_a}=\frac{4×68.2×10^3×1000×10^{-3}}{\pi×(40×10^{-3})^2×206×10^9}=0.26[mm]\]