今回は熱応力について学びましょう。
金属には熱を加えると膨張するという特徴があります。
では、傍聴できないように金属を押さえつけるとどのような力が生じるのでしょうか?
それが、今回解説する熱応力なのです。
前回の記事はこちらからどうぞ!

熱膨張
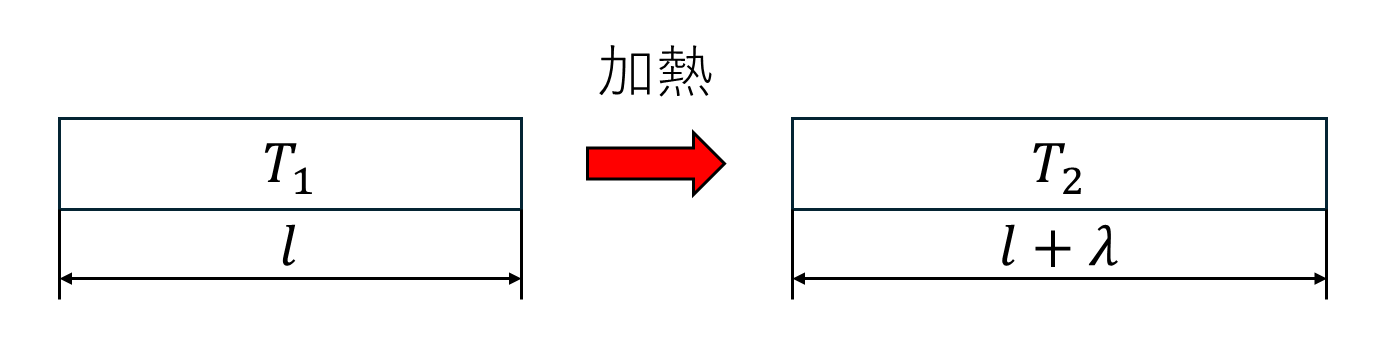
下図のように、金属でできた部材は温度が上昇すると、体積が膨張するという性質があり、これを『熱膨張』といいます。
熱膨張により、どれくらい体積が膨張するかは材料によって異なり、その膨張率を表したものを『熱膨張係数(線膨張係数)』といいます。
熱応力
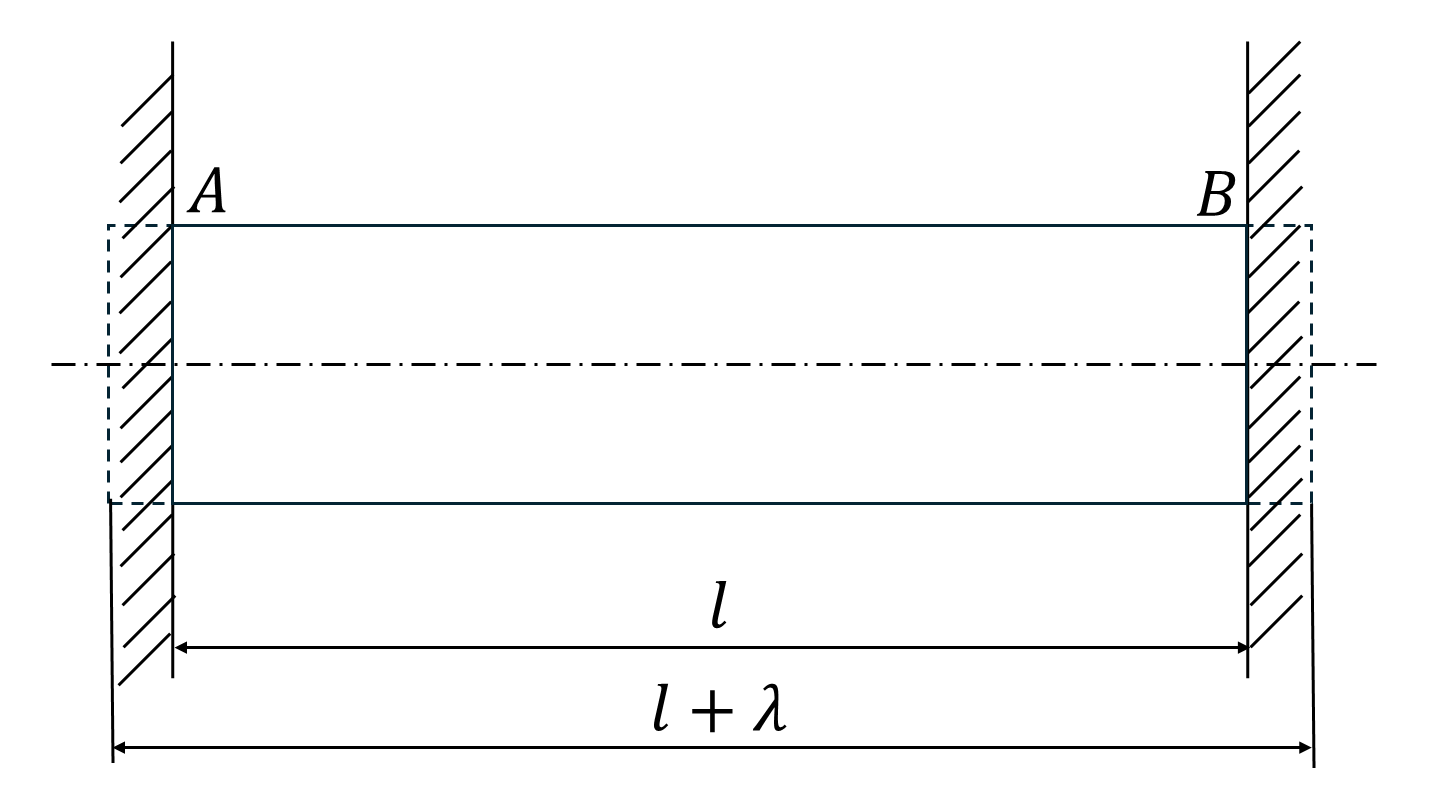
下図のように部材の両端を固定し、温度を上昇させることを考えます。
本来であれば熱膨張によって部材が変形するはずですが、壁に拘束されているため変形は不可能です。しかし、代わりに外力が作用したかのように部材内部に応力が生じます。
これを『熱応力』といいます。
改めて下図の状態で生じる熱応力について考えてみましょう。
温度が\(T_1\)から\(T_2\)まで加熱されたとして、部材の熱膨張係数を\(\alpha\)とすると本来の棒の伸び\(\lambda\)は、
\[\lambda=\alpha{l}(T_2-T_1)\]
これから圧縮ひずみをもとめると、
\[\varepsilon=\frac{\lambda}{l}=\frac{\alpha{l}(T_2-T_1)}{l}=\alpha{l}(T_2-T_1)\]
よってフックの法則により、熱応力(圧縮応力)は次のように定義されます。
\[\sigma=E\varepsilon=E\alpha(T_2-T_1) E:縦弾性係数\]
練習問題
問題
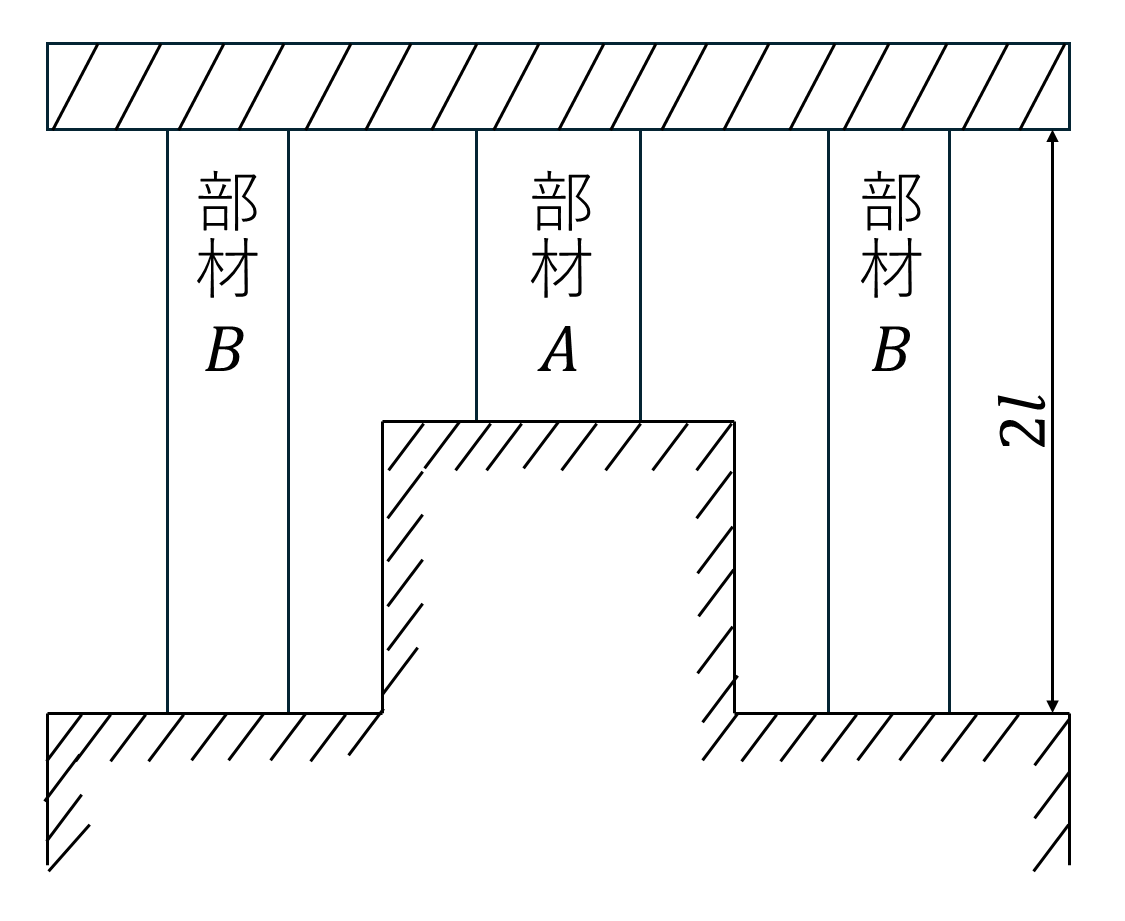
下図のように、長さ\(l\)、直径\(d_A\)の部材Aと長さ\(2l\)、直径\(d_B\)の2本の部材Bが剛体板に固定されている状態を考える。ここで温度が\(\Delta{T}\)変化したときに生じる荷重\(F_A,F_B\)と全体の伸び\(\lambda\)を求めなさい。ただし、\(l=500[mm],d_A=50[mm],\)\(d_B=30[mm],\Delta{T}=20[℃]\)、両部材の縦弾性係数及び熱膨張係数は共通で\(E=206[GPa],\alpha=11.6[10^{-6}/K]\)とする。
解くためのコツ
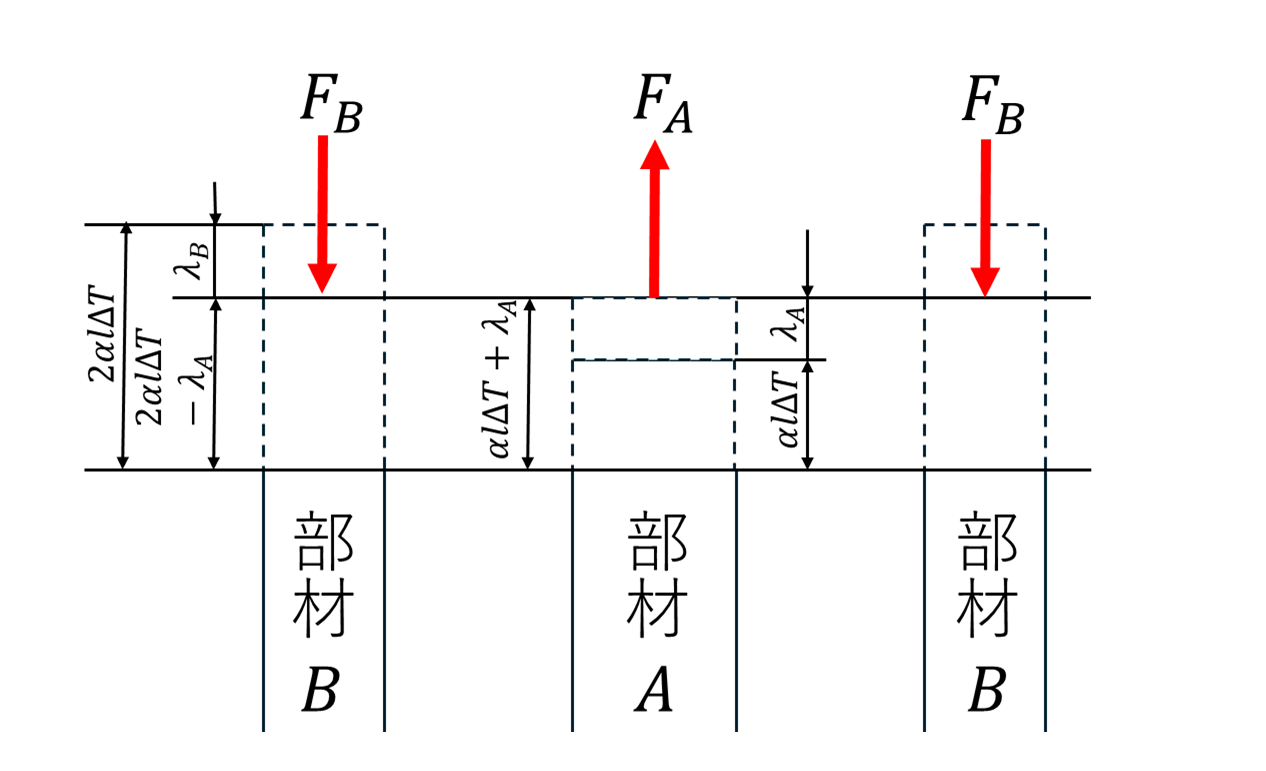
温度が上昇すると部材A、Bは下図のように変位します。
部材A、Bは同じ剛体板で固定されているため、同じだけ変位します。
しかし、それぞれの部材は熱膨張係数は同じですが、長さが違うため本来の伸びる量は異なります。
なので、力のつりあいをとる為に部材Aには引張の荷重\(F_A\)、部材Bには圧縮の荷重\(F_B\)が生じるのです。
解答と解説
荷重\(F_A,F_B\)を求めるために力のつりあい式を立てると、
\[F_A=2F_B (1)\]
一つの関係式に対して未知数が2つあるので不静定問題である。
部材A、Bの本来の熱膨張量は、
\[\begin{cases}{部材Aの熱膨張量:\alpha{l}\Delta{T}}\\{部材Bの熱膨張量:2\alpha{l}\Delta{T}}\end{cases}\]
\(F_A\)による部材Aの伸びを\(\lambda_A\)、\(F_B\)による部材Bの縮みを\(\lambda_B\)とすると、全体の伸び\(\lambda\)は、
\[\lambda=\alpha{l}\Delta{T}+\lambda_A=2\alpha{l}\Delta{T}-\lambda_B (2)\]
となり、この式(2)を変形すると、
\[\lambda_A+\lambda_B=\alpha{l}\Delta{T} (3)\]
フックの法則により、
\[\lambda_A=\frac{4F_A{l}}{\pi{d_A}^2{E}} \lambda_B=\frac{8F_B{l}}{\pi{d_B}^2{E}} (4)\]
式(4)を式(1)に代入すると、
\[\frac{\pi{d_A}^2{E\lambda_A}}{4l}=\frac{\pi{d_B}^2{E\lambda_B}}{4l}\]
\[{d_A}^2\lambda_A={d_B}^2\lambda_B\]
\[\lambda_A=\left(\frac{d_B}{d_A}\right)^2\lambda_A \lambda_B=\left(\frac{d_A}{d_B}\right)^2\lambda_B (5)\]
式(5)を式(3)に代入すると、求めたい\(\lambda_A,\lambda_B\)は、
\[\lambda_A\left\{1+\left(\frac{d_A}{d_B}\right)^2\right\}=\lambda_B\left\{1+\left(\frac{d_B}{d_A}\right)^2\right\}=\alpha{l}\Delta{T}\]
\[\lambda_A=\frac{\alpha{l}\Delta{T}}{1+\left(\frac{d_A}{d_B}\right)^2}=\frac{11.6×10^{-6}×500×10^{-3}×20}{1+\left(\frac{50}{30}\right)^2}=3.07×10^{-5}[m]=0.03[mm]\]
\[\lambda_B=\frac{\alpha{l}\Delta{T}}{1+\left(\frac{d_B}{d_A}\right)^2}=\frac{11.6×10^{-6}×500×10^{-3}×20}{1+\left(\frac{30}{50}\right)^2}=8.53×10^{-5}[m]=0.085[mm]\]
よって、全伸び\(\lambda\)は、
\[\lambda=\alpha{l}\Delta{T}+\lambda_A=11.6×10^{-6}×500×10^{-3}×20+3.07×10^{-5}=1.47×10^{-4}[m]=14.7[mm]\]
求めた\(\lambda_A,\lambda_B\)の値を式(4)に代入すると、\(F_A,F_B\)は、
\[F_A=\frac{\pi{d_A}^2E\lambda_A}{4l}=\frac{\pi×(50×10^{-3})^2×206×10^9×3.07×10^{-5}}{4×500×10^{-3}}=2.48×10^4[N]=24.8[kN]\]
\[F_B=\frac{\pi{d_B}^2E\lambda_B}{8l}=\frac{\pi×(30×10^{-3})^2×206×10^9×8.53×10^{-5}}{8×500×10^{-3}}=1.24×10^4[N]=12.4[kN]\]
まとめ
今回は『熱応力の概略と定義』について解説しました。
設計において摩擦などを考えると熱応力は密接にかかわっています。
しっかりと理解しておきましょう。
次回は『初期応力と応力集中』について解説していきます。
ここまで見ていただき、ありがとうございました!








コメント