今回は部材の様々な応力と変形の例を見ていきましょう。
例えば、これまでは部材の自重を考えずに応力や伸びを求めてきました。
では、自重を考慮に入れるときはどのように考えれば良いのでしょうか?
次の問題を解きながら考えていきましょう。
前回の記事はこちらからどうぞ!

自重を考慮したときの応力と変形
問題
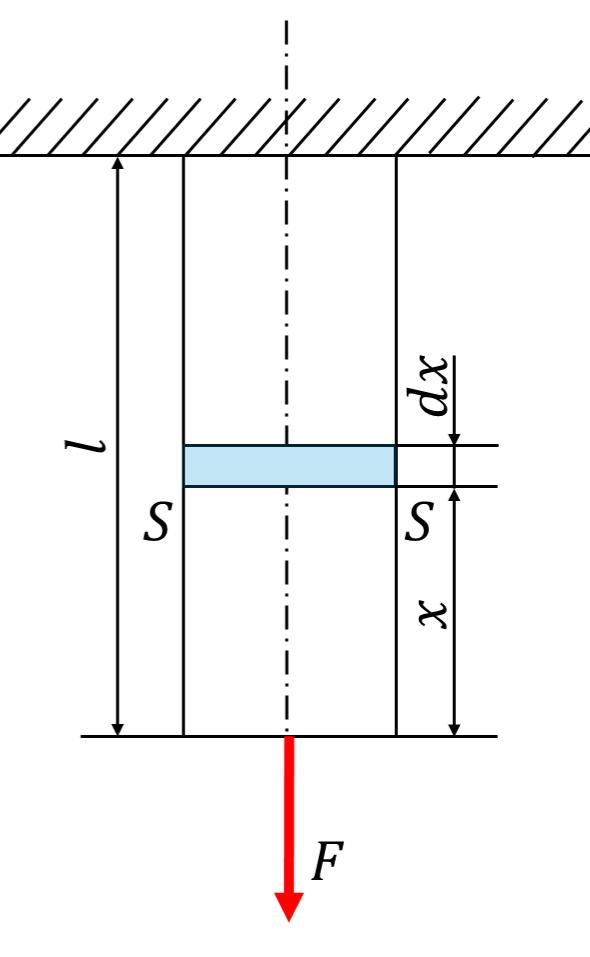
下図のような長さ\(l\)、断面積\(A=150[mm^2]\)の部材を天井に固定し、下端に\(F=500[N]\)の荷重が作用している。自重による応力を考慮し、部材に生じる最大応力\(\sigma_{max}=150[MPa]\)となるときの部材の長さ\(l\)と伸び\(\lambda\)を求めなさい。ただし、部材の材料の比重量は\(\gamma=7.8×10^{-5}[N/mm^3]\)、縦弾性係数E=206[GPa]とする。
解答と解説
問題を解く前に、比重量について復習しておきましょう!
比重量 \(\gamma [N/m^3]\):ある物質の単位体積当たりの重量を表す物質量
断面Sに作用する応力を考えると、下方の部材の重量と荷重Fが作用するので、次のように表せます。
\[\sigma=\frac{F+\gamma{A}x}{A}=\frac{F}{A}+\gamma{x}\]
ここで、\(x=l\)のとき応力が最大となるので、
\[\sigma_{max}=\frac{F}{A}+\gamma{l}\]
よって、求めたい長さ\(l\)は、
\[l=\frac{1}{\gamma}\left(\sigma_{max}+\frac{F}{A}\right)=\frac{1}{7.8×10^4}\left(150×10^6+\frac{500}{150×10^{-4}}\right)=1924[m]\]
ここで、断面Sに隣接する長さ\(dx\)の微小部分で生じる伸びを考えると、次のように表せます。
\[d\lambda=\frac{\sigma}{E}dx=\frac{1}{E}\left(\frac{F}{A}+\gamma{x}\right)dx\]
ここで、微小部分の伸び\(d\lambda\)を\(0\)から\(l\)の範囲で積分すれば、全体の伸びを求められるので、
\[\lambda=\displaystyle \int {d\lambda} =\frac{1}{E}\displaystyle \int_0^l \left({\frac{F}{A}+\gamma{x}}\right) dx=\frac{1}{E}\left[\frac{F}{A}x+\frac{1}{2}\gamma{x}^2\right]^l _0=\frac{1}{E}\left(\frac{Fl}{A}+\frac{1}{2}\gamma{l}^2\right)=\frac{l}{AE}\left(F+\frac{1}{2}Al\gamma\right)=\frac{1924}{150×10^{-4}×206×10^9}\left(500+\frac{1}{2}×150×10^{-4}×1924×7.8×10^4\right)=0.701[m]=701[mm]\]
テーパー付き円柱の応力と変形
問題
下図のような直径が連続的に変化する円柱を考える。ここで、両端に荷重\(F\)が作用するとき、\(x\)の位置に生じる応力と全体の伸び\(\lambda\)を求めなさい。ただし、円柱の左右の直径はそれぞれ\(d_1=30[mm],d_2=50[mm]\)、縦弾性係数\(E=206[GPa]\)、\(l=1000[mm]\)、\(F=80[kN]\)とする。

解答と解説
直径は直線的に変化するので\(x\)の位置での直径\(d(x)\)及び断面積\(A(x)\)は、
\[d(x)=\frac{d_2-d_1}{l}x+d_1,A(x)=\frac{\pi{d^2(x)}}{4}=\frac{\pi}{4}\left(\frac{d_2-d_1}{l}x+d_1\right)^2\]
よって求めたい応力\(\sigma(x)\)は、
\[\sigma(x)=\frac{F}{A(x)}=\frac{4F}{\pi\left(\frac{d_2-d_1}{l}x+d_1\right)^2}\]
ここで、微小長さ\(dx\)の伸び以下のようになる。
\[d\lambda=\frac{Fdx}{A(x)E}\]
そして、\(x\)の位置での断面積\(A(x)\)を計算簡略のため次のように置く。
\[A(x)=a(mx+n)^2 \begin{cases}{m=\frac{d_2-d_1}{l}}\\{n=d_1}\end{cases}\]
よって、求めたい全体の伸び\(\lambda\)は、
\[\lambda=\int{d\lambda}=\int_0^l\frac{Fdx}{A(x)E}=\frac{F}{E}\int_0^l\frac{1}{A(x)}dx=\frac{4F}{\pi{E}}\int_0^l\frac{1}{(mx+n)^2}=-\frac{4F}{\pi{Em}}\left[\frac{1}{mx+n}\right]^l_0=-\frac{4F}{\pi{Em}}\left(\frac{1}{ml+n}-\frac{1}{n}\right)=-\frac{4Fl}{\pi{E}(d_2-d_1)}\left(\frac{1}{d_2}-\frac{1}{d_1}\right)=\frac{4Fl}{\pi{E}(d_1-d_2)}\left(\frac{d_1-d_2}{d_1d_2}\right)=\frac{4Fl}{\pi{E}d_1d_2}=\frac{4×80×10^3×1000×10^{-3}}{\pi×206×10^9×30×10^{-3}×50×10^{-3}}=0.33[mm]\]
生じる応力が一様な部材の変形
問題
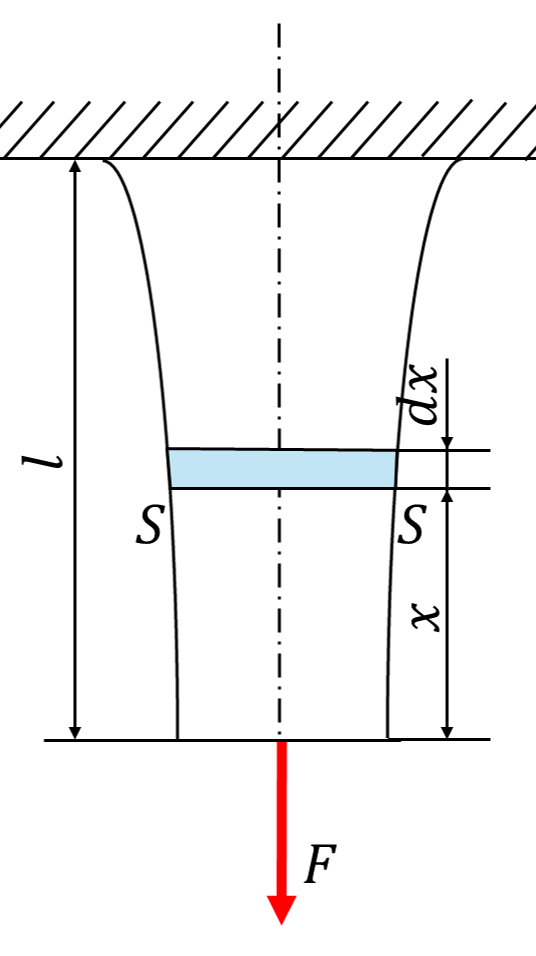
下図のような自重を考慮したときに、\(x\)がどの位置であっても許容応力\(\sigma_a\)(許容応力\(\sigma_a\)は最大応力\(\sigma_{max}\)と等しいとする。)であるような長さ\(l\)の部材を考える。ここで、部材の下端に荷重Fが作用するとき、\(x=\frac{l}{4}\)の位置での断面積\(A\)を求めなさい。ただし、長さ\(l=1000[mm]\)、下端の断面積\(A_0\)、許容応力\(\sigma_a=100[MPa]\)、荷重\(F=10[kN]\)、比重量\(\gamma=7.8×10^4[N/m^3]\)とする。
解答と解説
下図のように微小長さ\(dx\)の部分における力のつりあい式を立てると、
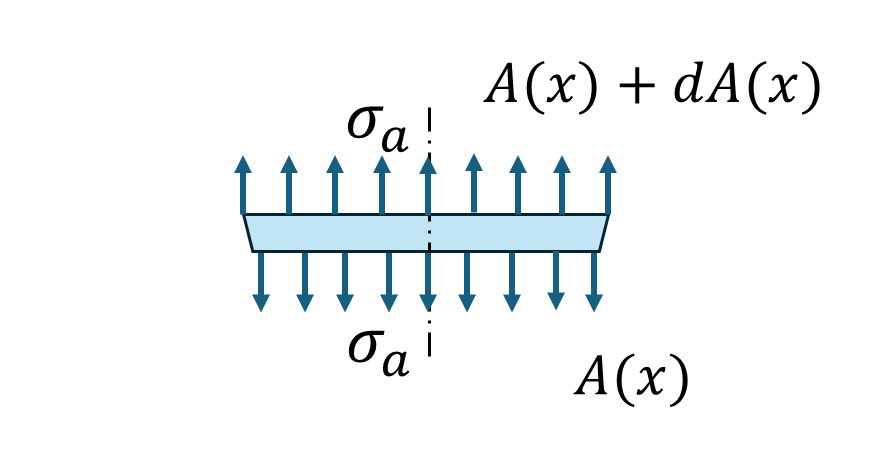
\[\sigma_aA(x)+\gamma{A(x)dx}=\sigma_a\{A(x)+dA(x)\}\]
\[\frac{1}{A(x)}dA(x)=\frac{\gamma}{\sigma_a}dx\]
両辺を積分すると
\[lnA(x)=\frac{\gamma{x}}{\sigma_a}+C\]
\[A(x)=C_1e^{\frac{\gamma{x}}{\sigma_a}} C_1=e^C\]
ここで、\(x=0\)のとき\(A(x)=A_0\)なので\(C_1=A_0\)。そして、下端の断面積\(A_0\)は\(A_0=\frac{F}{\sigma_a}\)で求められるので、\(x\)の位置での断面積A(x)は、
\[A(x)=C_1e^{\frac{\gamma{x}}{\sigma_a}}=A_0e^{\frac{\gamma{x}}{\sigma_a}}=\frac{F}{\sigma_a}e^{\frac{\gamma{x}}{\sigma_a}}\]
よって、求めたい\(x=\frac{l}{4}\)の位置での断面積\(A\)は、
\[A=\frac{F}{\sigma_a}e^{\frac{\gamma{\frac{l}{4}}}{\sigma_a}}=\frac{10×10^3}{100×10^6}e^{\frac{7.8×10^4×250×10^{-3}}{100×10^6}}=100[mm^2]\]
まとめ
今回は様々な状態における部材の応力とその変形について解説しました。
自重を考慮した問題やテーパー棒の変形問題は学校のテストでもよく出題されるのでしっかり復習しておきましょう。
次回は「引張圧縮の不静定問題」について解説していきます。
ここまで見ていただき、ありがとうございました!








コメント